O que é Semirreta?

Conhecer o conceito de semirreta é essencial para quem está se preparando para provas como a do Enem e vestibulares. Esse conceito está ligado, intimamente, com conceitos como reta, plano e espaço. Lembrando que tais conceitos são essenciais para a Geometria.

Semirreta: conceito da Geometria

Semirreta, semiplano e semiespaço são conceitos essenciais da Geometria por estarem relacionados com reta, plano e espaço. São empregados para explicar alguns casos e propriedades especiais. Confira a seguir a explicação desses conceitos.

O que é semirreta?

Antes de explicar o conceito de semirreta, precisamos relembrar o que é reta. Uma reta consiste em um conjunto infinito de pontos. Esse conjunto é ilimitado e não faz nenhuma curva, não tem “buracos”.

Agora que relembramos, o que é uma reta podemos responder a pergunta acima, o que é uma semirreta? Uma semirreta corresponde a uma porção de uma reta com início em um ponto qualquer que segue para uma de duas direções.

Algo interessante de pontuar, é que um ponto divide uma reta em duas semirretas. Confira as imagens abaixo:

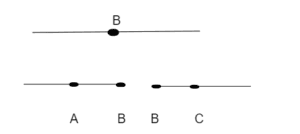
Acima temos semirretas representadas pela letra S maiúscula. Além disso, elas apresentam um ponto inicial e um ponto a que se direciona. Sendo assim, temos:

Semirreta SBA;
Semirreta SBC.

O ponto A faz parte de toda a reta, porém, não pertence à semirreta SBC. Por sua vez, o ponto C faz parte de toda a reta, porém, não se encontra na semirreta SBA.

O que é segmento de reta?

Outro conceito importante de abordar é o de segmento de reta. Consiste em uma parte da reta que é marcada por dois pontos. Os pontos que fazem parte de uma reta são nomeados por uma letra maiúscula.

O que é semiplano?

Para compreendermos o conceito de semiplano, é essencial entender o conceito de plano. Os planos consistem em superfícies infinitas e ilimitadas que não fazem curva. Os semiplanos surgem a partir da divisão de um plano em duas partes por uma reta.

Logo, o plano terá início, mas não terá fim. Então, uma das suas propriedades é se dois pontos (A e B) se encontram no mesmo semiplano, todos os pontos do segmento de reta AB também estarão nesse semiplano.

Também devemos considerar que se dois pontos (A e B) se encontram em semiplanos distintos, então a reta que contém A e B é concorrente à reta que dividiu o plano. Confira a figura abaixo, em que um plano está dividido em dois semiplanos:

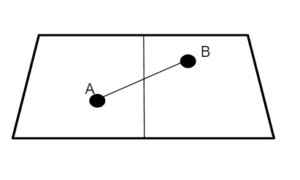
Semiplanos podem ser usados para definir polígonos convexos. Isso é possível desde que todo o polígono se encontre em um mesmo semiplano formado por cada um dos seus lados. Confira um exemplo prático de um polígono convexo na figura abaixo:

O que é semiespaço?

Mais uma vez é importante contextualizar o conceito de origem, ou seja, precisamos explicar o que é espaço. Por definição, o espaço é o conjunto de todos os planos. Logo, é infinito e ilimitado para todas as direções e nele estão contidas todas as figuras e formas geométricas. Basicamente, o espaço é formado por tudo a nossa volta.

O semiespaço surge quando uma reta divide o espaço em duas partes. Essas partes passam a ser chamadas de semiespaços. Para que fique mais claro esse conceito pedimos que você imagine uma caixa de sapatos que consiste em uma pequena parcela do espaço.

Caso essa caixa seja dividida ao meio por um plano, então teremos duas metades que irão representar semiespaços. Uma função importante dos semiespaços é que podem ser usados para determinar os poliedros convexos.

Então se cada face do poliedro está situada em um plano que determina dois semiespaços e o poliedro está todo contido em um desses semiespaços, temos um poliedro convexo. Por isso esse conceito é tão importante para a geometria.

Resumindo

Semirretas são uma parte importante dos estudos da geometria. Elas possuem um ponto de origem que indica o seu início. Contudo, elas não têm fim, isto é, são infinitas. A representação das semirretas tem a indicação de uma seta em um dos lados que demonstra o sentido infinito.

Importante

Antes da prova de matemática do Enem e vestibulares é importante repassar os conceitos básicos de geometria. Além de esses conceitos poderem ser abordados diretamente podem fazer parte de uma questão. Dessa forma é essencial entendê-los para poder entender a proposta das questões.

Essa é uma forma de garantir mais chances de acerto e também é interessante para a vida. A geometria nos ajuda a entender melhor o mundo à nossa volta e desenvolver uma relação mais prática com o entorno.

Curiosidade

Temos uma curiosidade da Língua Portuguesa a respeito de semirretas. Antes do Novo Acordo Ortográfico, essa palavra era escrita “semi-reta”, mas atualmente a forma correta é semirreta.

Gostou de saber mais sobre semirreta? Para conferir mais conteúdos como este e dicas para o Enem e o vestibular, acesse outros posts do blog Hexag!